При решении очередной технической задачи потребовалось найти уравнение прямой по зашумленным выборкам АЦП. Фактически данная статейка является упрощением предыдущей, поэтому все пояснения можно почерпнуть там. В этой статье представлены только формулы и конечный результат.
Решение.
Запишем уравнение прямой в виде:
Результаты изменений произвольно пронумеруем и занесем в таблицу:
| Номер измерения i | Результат измерения величины x | Результат измерения величины y |
| 1 | x1 | y1 |
| 2 | x2 | y2 |
| … | … | … |
| N | xN | yN |
Нумерация точек может быть произвольной, главное сохранить пары точек .
Критерий решения можно записать так:
Для расчета используем Метод Наименьших Квадратов:
Введем обозначение:
Получаем систему уравнений:
Та же система уравнений в матричной форме:
Решение системы уравнений:
Решение:
Вычисления в Microsoft Excel:
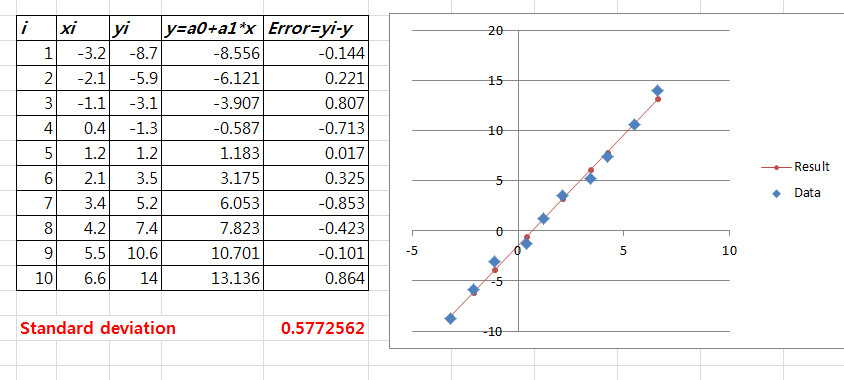
Готовый файл: Line.xls.
Подобные статьи: Как найти параметры параболы по результатам измерений?
